In Bayesian deep learning, we infer a posterior distribution over the weights of the network. This provides a variety of improvements over typical neural networks, whose outputs come from maximum likelihood (point) estimates of the parameters.

If you’re new to Bayesian neural nets, you might be a bit disappointed as I won’t derive the whole framework here (read the original paper, Bayes by Backprop (Blundell et al., 2015), if you’re interested!). However, I’ll restate the important parts; if you’re not new to probability, they should make intuitive sense, so you’re not missing much.

The big idea is that we need to infer a posterior \(p( \boldsymbol w \mid \mathcal D) \) over the weights. Why? Because then we can make predictions via the predictive distribution \[p(y \mid \boldsymbol x, \mathcal D) = \int p(y \mid \boldsymbol x, \boldsymbol w) \, p(\boldsymbol w \mid \mathcal D) \, \mathrm d \boldsymbol w.\]Note that the right-hand side of this equality is \(\mathbb E_{p(\boldsymbol w \mid \mathcal D)}[p(y \mid \boldsymbol x, \boldsymbol w)]\). And \(p(y \mid \boldsymbol x, \boldsymbol w)\) is just our neural network output, which means if we did a good sampling across all possible weights according to this posterior, we could estimate our predictive distribution. As you might imagine, this is intractable due to infinitude of weight settings

So what do we do? We choose an approximation \(q(\boldsymbol w \mid \theta)\) (we call this the variational posterior) with parameters \(\theta\) that we'll use to approximate the true posterior \(p(\boldsymbol w \mid \mathcal D)\). The optimal \(\theta\) will make these distributions as close as possible, hence we have \[ \theta^* = \arg \min_\theta \operatorname{KL}[q(\boldsymbol w \mid \theta) \, \vert \vert \, p(\boldsymbol w \mid \mathcal D)] \] where \( \operatorname{KL}[\cdot \, \vert \vert \, \cdot ]\) denotes the Kullback-Leibler divergence. It turns out that

\[\begin{align} \theta^* &= \arg \min_\theta \operatorname{KL}[q(\boldsymbol w \mid \theta) \, \vert \vert \, p(\boldsymbol w \mid \mathcal D)] \\ &= \arg \min_\theta \operatorname{KL}[q(\boldsymbol w \mid \theta) \, \vert \vert \, p(\boldsymbol w)] - \mathbb E_{q(\boldsymbol w \mid \theta)}[\log p(\mathcal D \mid \boldsymbol w)] \\ &\approx \arg \min_\theta \sum_{w_i \sim q(\boldsymbol w \mid \theta)} \log q(\boldsymbol w_i \mid \theta) - \log p(\boldsymbol w_i) - \log p(\mathcal D \mid \boldsymbol w_i) \end{align} \]

Intuitively, we want \(q(\boldsymbol w \mid \theta)\) not to be too inconsistent with our prior, but we also want it to actually describe the data well, so the second equality isn’t too surprising.

One last thing worth mentioning: as you see above, we're sampling weights from a distribution. It's unclear how to backprop through a random node with respect to the parameters of the weight distribution, which is why we perform what's called the reparametrization trick. The “trick” is that we introduce a new parameter \(\epsilon\) and reparameterize our random samples in a way that allows backprop to flow through the deterministic nodes. This is best demonstrated with a normal distribution. Say we want to sample weights from \(N(\mu, \sigma)\). The important thing to realize here is that all normal distributions are just scaled and translated versions of \(N(0, 1)\)! With this in mind, the deterministic transformation we can make on a sampled \(\epsilon \sim N(0,1) \) to simulate our weight distribution \(N(\mu, \sigma)\) is \[ w_i = \mu_i + \sigma_i \cdot \epsilon \] Now our sample looks like it's drawn from our specific distribution, but we can still differentiate with respect to (and therefore optimize) \(\mu\) and \(\sigma\) after performing operations using \( w \).

Now for the (even more) interesting stuff! One of the first things I wondered when reading the seminal paper was "why a Gaussian?". Yeah, yeah, most things are distributed normally. Yes, I know Gaussians have nice properties and are easy to reparametrize, as we saw above. But why can't my weight distribution be skewed towards (say) positive weights? That's where the Kumaraswamy distribution comes in.

The Kumaraswamy double bounded distribution is a distribution [family] defined on \((0,1)\). It's similar to the beta distribution, but it's far, far simpler to deal with. It’s also really flexible, giving several shapes depending on one’s choice of parameters:

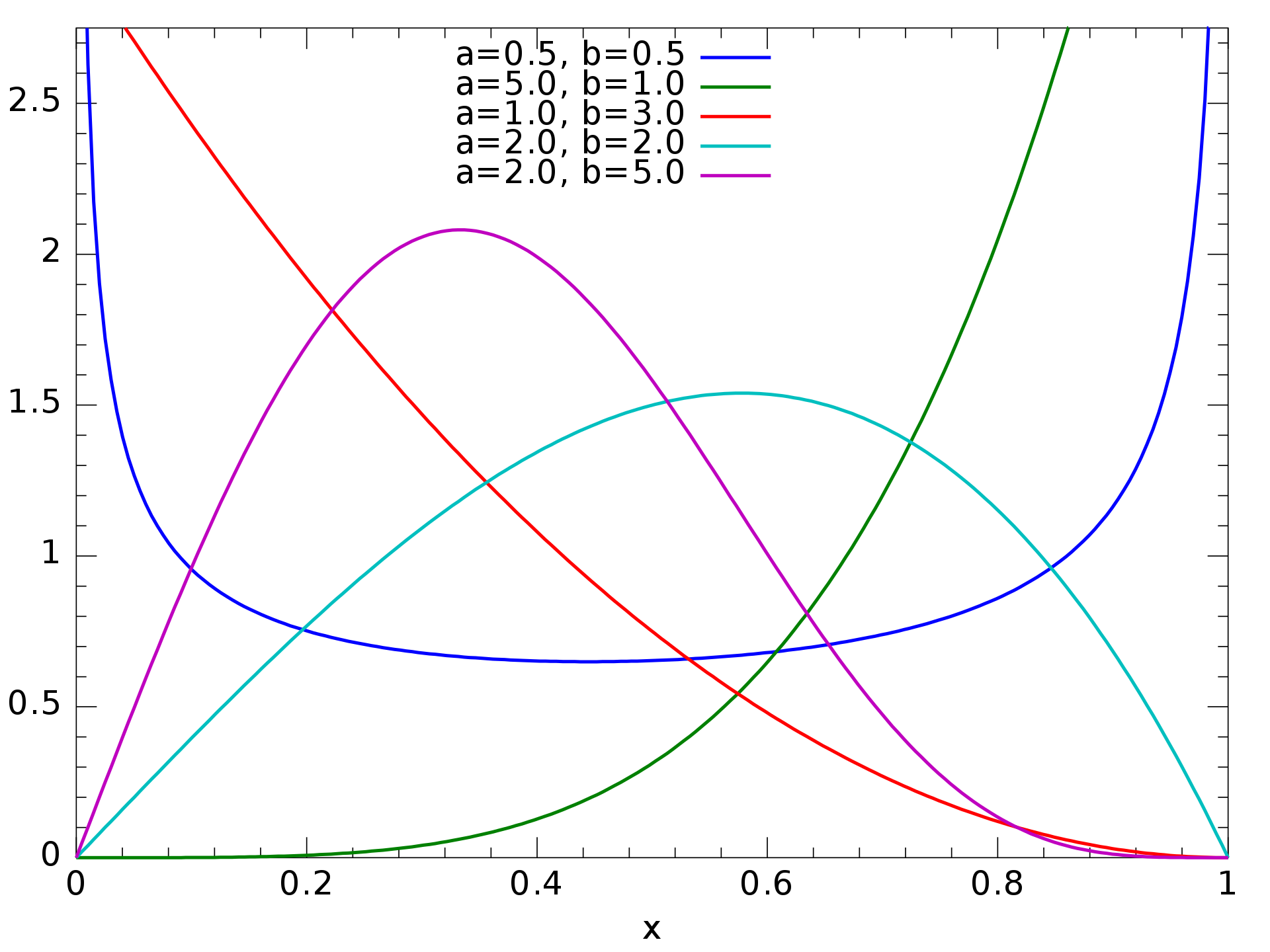
The probability density is given by \[ f(x;a,b)=abx^{a-1}{(1-x^{a})}^{b-1} \] for positive \( a, b \). Between its flexibility and simplicity, I thought it was a pretty good choice for a weight distribution.

Part of what makes this an interesting distribution to use is the fact that we can’t say that all Kumaraswamy distributions are shifts/rescalings of another, standard distribution. It took a while to think of a way to sample from this distribution in a backpropable way. Recall that our goal is to sample a noise variable \( \epsilon \) from a simple distribution of our choice (like a standard Gaussian). We want to apply a deterministic transformation \(T(\epsilon; a,b) \) that sends the random noise onto a distribution equivalent to \( \operatorname{Kumaraswamy}(a, b) \).

What’s a good way to simulate a given distribution with a simpler one? One way is to make use of the ideas underpinning inversion sampling. The main idea behind it is that if \(Y\) follows a standard uniform distribution and if \(X\) has a cumulative distribution \(F_{X}\), then the random variable \(F_{X}^{-1}(Y)\) has the same distribution as \(X\). If we apply this idea, then we can use \[ T(\epsilon; a,b) = F^{-1}(\epsilon; a, b), \] where \(F^{-1}\) is the Kumaraswamy inverse cumulative distribution (i.e. quantile) function and let \[ \epsilon \sim U(0,1), \] the standard uniform distribution. Given an \( \epsilon \), \(T\) is clearly deterministic, and by the inversion sampling rule, it will give us back \( \operatorname{Kumaraswamy}(a, b) \) when applied to \(\epsilon\). Perfect! Last thing we need to check: is the transform differentiable? It absolutely is: integrate the PDF and invert to get \[ T(\epsilon; a,b) = F^{-1}(\epsilon; a, b) = \sqrt[a]{1- \sqrt[b]{1-x} } \] which isn’t a pain to differentiate (especially if you’re an automatic differentiation package).

Now that we’re on solid theoretical ground, we implement this as our variational posterior and optimize as discussed above. Note: as we want to limit weights between \(-1\) and \(1\) (not \(0\) and \(1\)), we actually scale and shift the distribution for our purposes. To be specific, we actually sample from \( 2 \cdot \operatorname{Kumaraswamy}(a, b) - 1\), but this doesn't change much of the math. And just like that, we have a flexible distribution that performs with equal overhead compared to the Gaussians used in the original paper.

Just for fun, we can take it one step further and think about variational posteriors that are infinitely flexible (in a universal approximation sense). What if we used an additional (vanilla) neural network to learn the distribution? Of course, this can have some (potentially serious) training and computational overhead, but it's still cool to think about!

(It would be an interesting extension to find out what the minimum required width/depth is for approximating most (reasonable) distributions. Recall that for a network of depth \(d\) and width \(w\), the additional parameter cost scales like \(\Theta(w^2d)\), so discovering the minimum theoretical requirements would be valuable for reducing parameter burden.)

So how do we go about using a neural net as our posterior? We need to be able to sample from it in a parameterized manner and compute (log) probabilities (that's \(\log q(\boldsymbol w \mid \theta)\)) from it, given a setting of the weights. I could think of two ways to achieve this in general. If you can conceive of better approaches, I'm interested in knowing!

The first way is to make our neural net \(M_\theta\) allow us to do the same things we did with the Kumaraswamy distribution. For this, we need the network's output \(M(x)\) to be the \(F^{-1}(x)\), where \(F^{-1}\) is the quantile function of the distribution the net represents. Since a quantile function uniquely defines an associated pdf (given that \(F^{-1}\) is well-defined and monotonic in the interval \((0,1\)))^[1], we can sample from \(U(0,1)\), run the sample through our network, \(F^{-1}\), and get our sample. In other words, for sampling, \(\epsilon \sim U(0,1)\) and \(T(\epsilon; \theta) = M_\theta(\epsilon)\). This takes care of sampling from a pdf in a parameterized manner.

Now, how do we compute log probability given a setting of the weights? Well, the quantile function is the inverse of the cdf, and the pdf is the derivative of the cdf. Thus we have \[ q(\boldsymbol w | \theta) = \frac{\mathrm d}{\mathrm dx} \big((F^{-1})^{-1}(x)\big) = \frac{1}{F^{-1'}(F(x))}. \] How might we compute \(F\) given that we can only query \(F^{-1}\) and its derivative? This amounts to solving \(F^{-1}(t) = x\), since then \(F(x) = t\). For this, we just use the bisection method on \(F^{-1} = M_\theta\) on \((0,1)\)!

A second way is to use the neural network to parameterize the distribution directly (up to a constant) on the real line (or, more realistically, on \([-1, 1]\)). If \(M_\theta\) is nonnegative (and not identically zero) on \([-1, 1]\), then we must have that \(Z = \int_{-1}^1 M_\theta(x) \, \mathrm dx\) is positive and finite. Then \(M_\theta\) uniquely defines a valid pdf given by \[f(x) = \frac{1}{Z} M_\theta(x).\] We have a few options now. We can actually sample from \(f\) without knowing \(Z\) by using the Metropolis-Hastings algorithm. But to compute the (log) probability of an input (i.e. weights setting), we definitely (probably) need this normalization constant. Thankfully, there are some ways to do this that aren't too bad; just stay away from the harmonic mean estimator if you know what's good for you^[2].

Finally, with these approaches, we can infer a posterior that is as flexible as allowed by the neural network!

The code implementing the ideas in this post is available here!